[1]:
%reload_ext eradiate.notebook.tutorials
Last updated: 2024-03-07 15:48 (eradiate v0.25.1.dev31+g2a83b0ba.d20240229)
3D simulation basics#
Overview
In this tutorial, we introduce basic 3D simulation features. Eradiate is intrinsically a 3D radiative transfer model, and a lot of workflows and concepts introduced here are applicable to 1D simulations as well.
Prerequisites
Ability to run 1D simulations and visualise the results (see First steps with Eradiate).
What you will learn
How to set up and visualise a 3D scene.
How to compute the reflectance of a complex surface without an atmosphere.
We start by activating the IPython extension and importing and aliasing a few useful components. We also select the monochromatic mode.
[2]:
%load_ext eradiate
import matplotlib.pyplot as plt
import numpy as np
import eradiate
from eradiate import unit_registry as ureg
from eradiate import scenes as ertsc
eradiate.set_mode("mono")
We set the computational mode to monochromatic, since we will be simulating scenes without atmospheres. Hence the correlated-k distribution method will not be useful here.
Next we set up convenience functions for plotting BRF results and visualizing camera renders.
[3]:
def show_camera(
exp,
measure_id,
robust=True,
add_colorbar=False,
vmin=None,
vmax=None,
):
"""
Display the output of a monochromatic camera measure.
"""
_, ax = plt.subplots(1, 1)
exp.results[measure_id]["radiance"].squeeze(drop=True).plot.imshow(
ax=ax,
origin="upper",
cmap="Greys_r",
vmin=vmin,
vmax=vmax,
robust=robust,
add_colorbar=add_colorbar,
)
ax.set_aspect(1) # Ensures that pixels are represented as squares
plt.show()
plt.close()
def show_brf(exp, measure_id):
"""
Display the BRF output of a distant radiance measure.
"""
_, ax = plt.subplots(1, 1)
exp.results[measure_id]["brf"].squeeze(drop=True).plot(
ax=ax, x="vza", linestyle=":", marker="."
)
plt.show()
plt.close()
First 3D scene visualisation#
We start by creating a simple scene consisting only of a rectangular surface with Lambertian reflectance. Here, we must specify the horizontal extent of the surface because no parent scene element will constrain it. As soon as a canopy is assigned, this is no longer required (see below).
Note: We use the Eradiate unit registry ureg to attach the unit meter to the surface’s edge length.
[4]:
lambertian_surface=ertsc.surface.BasicSurface(
shape=ertsc.shapes.RectangleShape(edges=10.0 * ureg.m),
bsdf=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
)
Next, we create a perspective camera to visualise the surface.
[5]:
camera_oblique = ertsc.measure.PerspectiveCameraMeasure(
id="camera_oblique",
origin=[15, 15, 15] * ureg.m,
target=[0, 0, 0] * ureg.m,
up=[0, 0, 1],
film_resolution=(320, 240),
spp=512,
)
Now we create the experiment object. We use the CanopyExperiment class, specialised to handle 3D surface geometry without atmosphere. The illumination and canopy parameters are left to their default values: no canopy will be added above the surface, and the illumination will be directional, oriented towards the nadir.
[6]:
exp = eradiate.experiments.CanopyExperiment(
surface=lambertian_surface,
measures=camera_oblique,
)
We run the simulation and use the convenience function defined above to visualize the result.
[7]:
eradiate.run(exp)
show_camera(exp, "camera_oblique")
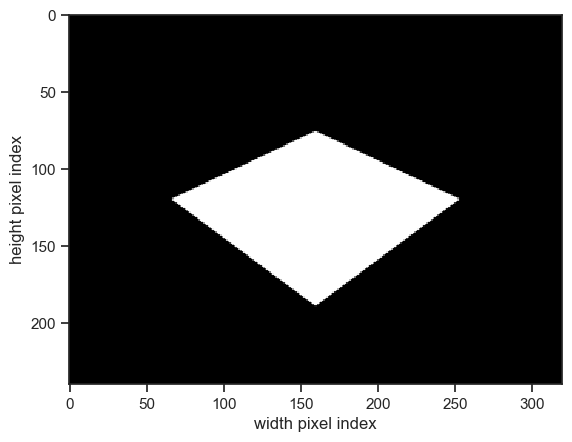
Adding a canopy#
Now, let’s add a canopy above this background surface. We start with a very simple homogeneous cloud of floating disks. The DiscreteCanopy class has a convenience constructor method homogeneous(), ideal for this case.
Note: The unit registry allows for intuitive numerical values for both the horizontal extent of the canopy as well as the radius of the floating leaves.
[8]:
homogeneous_canopy = ertsc.biosphere.DiscreteCanopy.homogeneous(
l_vertical=1.0 * ureg.m,
l_horizontal=10.0 * ureg.m,
lai=2.0,
leaf_radius=10 * ureg.cm,
)
We create a new experiment object, which contains the canopy we just defined.
Note: We can now define the surface through its BSDF only, because the size of the rectangular shape is defined by the width of the canopy.
[9]:
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
canopy=homogeneous_canopy,
measures=camera_oblique,
)
We run the experiment and display the result.
[10]:
eradiate.run(exp)
show_camera(exp, "camera_oblique")
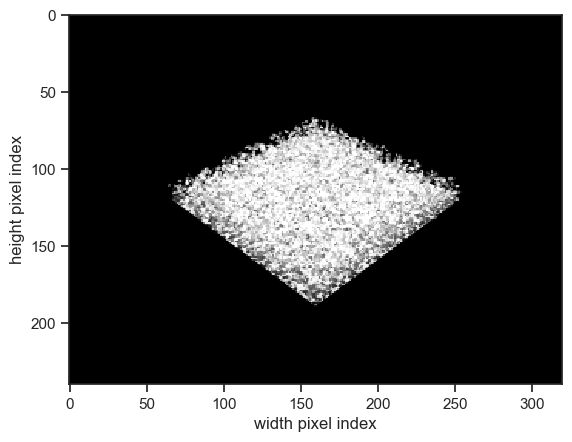
Top-of-canopy BRF computation#
Now that we know how to define a surface with a 3D geometry, let’s compute its reflectance. For a convenient visualisation, we will use a hemispherical distant measure. This measure computes the radiance leaving the scene at an infinite distance. Since we don’t have an atmosphere here, this is equivalent to computing the so-called “top-of-canopy” leaving radiance. The measure also derives the top-of-canopy reflectance.
[11]:
hdistant = eradiate.scenes.measure.HemisphericalDistantMeasure(spp=10000)
Here, we use the default parameters. In particular:
the
film_sizeis left to its default value, which is fairly low (32×32), and we therefore don’t expect a finely resolved view of the BRF;the
azimuth_conventionparameter is left unset, which means that the viewing azimuth angle added to the result dataset will use the default convention.
Now, let’s build and run an experiment using this sensor. We will set the illumination to a non-default value so that we can visualise some interesting features in the reflectance:
[12]:
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
illumination=ertsc.illumination.DirectionalIllumination(
zenith=30.0 * ureg.deg,
azimuth=45.0 * ureg.deg,
),
canopy=homogeneous_canopy,
measures=hdistant,
)
ds = eradiate.run(exp)
ds
[12]:
<xarray.Dataset> Size: 42kB
Dimensions: (sza: 1, saa: 1, w: 1, y_index: 32, x_index: 32)
Coordinates:
* sza (sza) float64 8B 30.0
* saa (saa) float64 8B 45.0
* w (w) float64 8B 550.0
* y_index (y_index) int64 256B 0 1 2 3 4 5 6 7 ... 24 25 26 27 28 29 30 31
y (y_index) float64 256B 0.0 0.03226 0.06452 ... 0.9355 0.9677 1.0
* x_index (x_index) int64 256B 0 1 2 3 4 5 6 7 ... 24 25 26 27 28 29 30 31
x (x_index) float64 256B 0.0 0.03226 0.06452 ... 0.9355 0.9677 1.0
vza (x_index, y_index) float64 8kB 86.47 86.47 86.47 ... 86.47 86.47
vaa (x_index, y_index) float64 8kB 225.0 222.1 219.2 ... 42.1 45.0
Data variables:
radiance (w, y_index, x_index, saa, sza) float64 8kB 0.262 ... 0.2621
brdf (w, y_index, x_index, saa, sza) float64 8kB 0.1585 ... 0.1586
brf (w, y_index, x_index, saa, sza) float64 8kB 0.4981 ... 0.4982
irradiance (sza, saa, w) float64 8B 1.652We can now visualise the data quickly using xarray’s built-in plotting facilities:
[13]:
ds["brf"].squeeze().plot()
[13]:
<matplotlib.collections.QuadMesh object at 0x7f12afea5100>
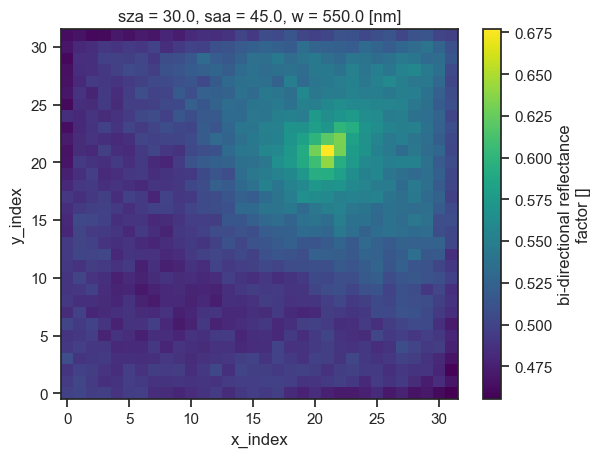
This plot maps the hemisphere to a square using the uniform_hemisphere_to_square() function. The horizontal and vertical axes are mapped to the 0° and 90° hemispherical planes, while the diagonals are mapped to the 45° and 135° hemispherical planes. We visualise the reflective hot spot in the illumination direction.
Arguably, this kind of raw data plot may confuse some viewers. We provide a complete tutorial covering how to plot hemispherical distant measure output (see Advanced visualisation).
We can also use a MultiDistantMeasure to compute the reflectance in the principal plane as we did in the First steps with Eradiate tutorial. Note also that the measure is configured to align with the illumination, which is set with an azimuth angle of 45°.
[14]:
mdistant = ertsc.measure.MultiDistantMeasure.hplane(
id="toa_brf",
zeniths=np.arange(-75, 76, 5),
azimuth=45 * ureg.deg,
srf={"type": "multi_delta", "wavelengths": 550.0 * ureg.nm},
spp=10000,
)
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
illumination=ertsc.illumination.DirectionalIllumination(
zenith=30.0 * ureg.deg,
azimuth=45.0 * ureg.deg,
),
canopy=homogeneous_canopy,
measures=mdistant,
)
ds = eradiate.run(exp)
ds
[14]:
<xarray.Dataset> Size: 2kB
Dimensions: (sza: 1, saa: 1, w: 1, y_index: 1, x_index: 31)
Coordinates:
* sza (sza) float64 8B 30.0
* saa (saa) float64 8B 45.0
* w (w) float64 8B 550.0
* y_index (y_index) int64 8B 0
y (y_index) float64 8B 0.0
* x_index (x_index) int64 248B 0 1 2 3 4 5 6 7 ... 23 24 25 26 27 28 29 30
x (x_index) float64 248B 0.0 0.03333 0.06667 ... 0.9333 0.9667 1.0
vza (x_index, y_index) int64 248B -75 -70 -65 -60 ... 60 65 70 75
vaa (x_index, y_index) int64 248B 45 45 45 45 45 ... 45 45 45 45 45
Data variables:
radiance (w, y_index, x_index, saa, sza) float64 248B 0.2564 ... 0.2857
brdf (w, y_index, x_index, saa, sza) float64 248B 0.1552 ... 0.1729
brf (w, y_index, x_index, saa, sza) float64 248B 0.4875 ... 0.5432
irradiance (sza, saa, w) float64 8B 1.652Visualisation is also greatly facilitated by xarray’s plotting features. We explicitly use the vza (viewing zenith angle) coordinate as the x coordinate. We see the retro-reflective “hot spot” in the illumination direction (30°). Also note how variance typical of Monte Carlo methods appears: it can be reduced by increasing the sample count of the measure (spp parameter).
[15]:
ds.brf.plot(x="vza");
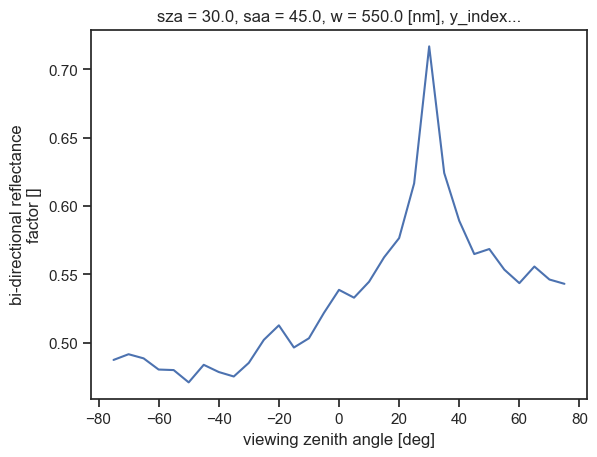
Padding the canopy with clones of itself#
A unit cell of canopy floating in the void is not something one could realistically encounter in the real wonder: in remote sensing, a point observed on Earth has surroundings. One way to create a surrounding environment for our canopy unit cell is to assume that it is in the middle of a “forest” with similar properties; or, in other words, that it is surrounded by clones of itself.
A conceptually simple way to visualise this is to imagine that our unit cell is periodically repeated indefinitely. However, Eradiate does not support such feature; instead, it allows the user to pad the unit scene with an arbitrary number of cheap (in terms of memory) clones.
This is controlled by the padding parameter of the CanopyExperiment class:
[16]:
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
canopy=homogeneous_canopy,
padding=1,
measures=camera_oblique,
)
Let’s run this experiment and visualise the results:
[17]:
eradiate.run(exp)
show_camera(exp, "camera_oblique")
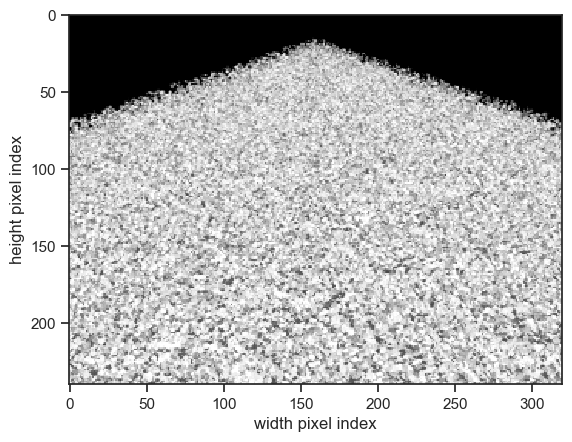
Our unit cell is now surrounded by a row of clones of itself: this amounts to 8 clones. Let’s increase padding to 2 (we now have 8 + 16 = 24 clones):
[18]:
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
canopy=homogeneous_canopy,
padding=2,
measures=camera_oblique,
)
eradiate.run(exp)
show_camera(exp, "camera_oblique", add_colorbar=True)
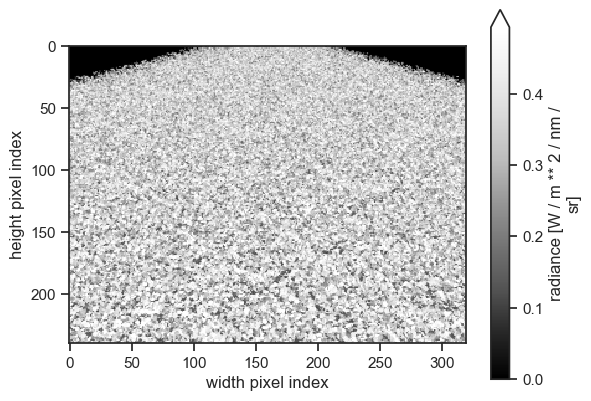
We can see that the rendering time increases with padding. This is due to more pixels of the final image requiring the simulation of multiple scattering and rendering time should become approximately constant with larger padding values:
[19]:
exp = eradiate.experiments.CanopyExperiment(
surface=ertsc.bsdfs.LambertianBSDF(reflectance=0.5),
canopy=homogeneous_canopy,
padding=25,
measures=camera_oblique,
)
eradiate.run(exp)
show_camera(exp, "camera_oblique", vmin=0.0, add_colorbar=True)
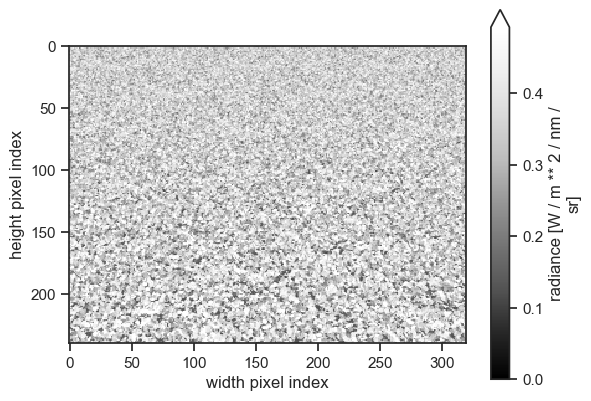
Final words#
This was just a quick overview of Eradiate’s 3D simulation features. This simple example can be expanded, for instance by computing the top-of-canopy reflectance of the canopy in the principal plane with different padding values to assess which amount of padding is required to converge to a periodic behaviour.